TORQUE, LAW OF SINES AND SUM OF MOMENTS
here’s a simulated crane boom supported by a green cable
that goes over a sheave (pulley) mounted in the tower.

The end of the cable is attached to a load cell
that is hooked to a turn-buckle which is anchored to the base.

GIVEN; the boom is 60″ long, weighs 6 lbs. ,
and makes a 25 deg angle with the horizontal.
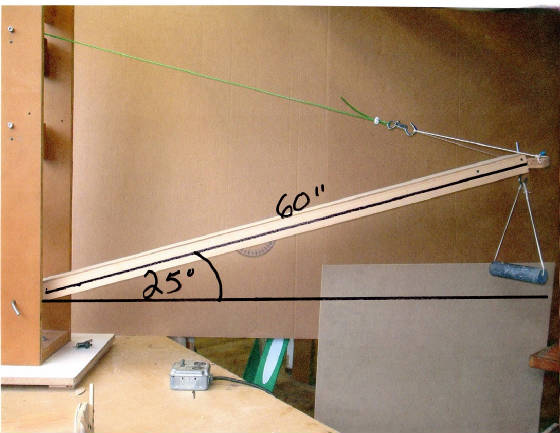
FIND: the tension in the boom line.
In the crane industry they use terms like
Overturning moment (OTM) and Righting moment.(RM)
Engineers use the formula for the sum of the moments.
We assume that since the boom is not moving, it is in
equilibrium.
That’s the basis for our formulas.
With the boom stationary, the moment pulling the boom
down, and the moment keeping it up at a 25 deg angle must
be equal- or the sum of the moments must equal zero.
The Moment pulling the boom down acting in a Clock-wise
direction (CW) added to the opposite moment
acting Counter Clock-wise (CCW) must equal zero.
We can simplify this by saying:
the CW Moment = CCW Moment.
Remember Moment = Force x Distance
The CW moment has 2 parts:
1-the moment that is causing the boom to fall-i.e. the lead cylinder
hanging from the tip of the boom. The cylinder weighs 6lbs. 13oz. or 109 oz.
The FORCE is the force of gravity acting on that 109 oz. load
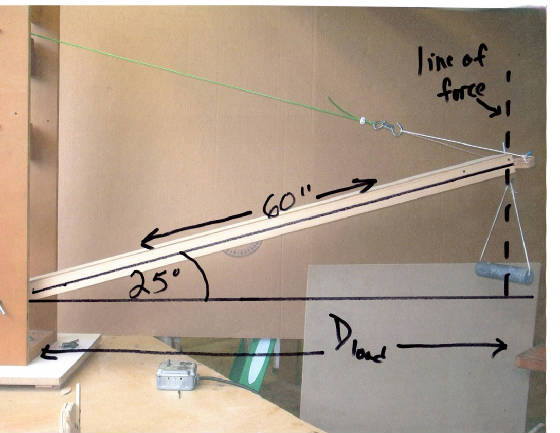
The DISTANCE is NOT 60″. With moment we’re interested in
the distance from the line of force to the pivot point.
The force of gravity pulls straight down on the boom. The direction
of that force ( the line of force ) is straight down.
We need to find the shortest distance from somewhere along
that line to the pivot point.
You can see from the picture below that the perpendicular
distance from the line to the pivot is the shortest.
That will be D(load).
In this rt. triangle, we have an hypotenuse of 60″,
and a base angle of 25 deg. To find D(load) we’ll
use the cosine function.
Cos 25 = D (load) / 60 cos 25 = .9063
solving we get
D(load) = .9063 x 60 or
D(load) = 54.378 inches
now back to the basic equation M = F x D
M = 109 oz. x 54.378″
M = 5927.202 inch ounces
2- the next part of the moment is the boom itself.
Don’t forget it weighs almost as much as the load (6lbs.)
and it is also pulling down on the cable. So
M(boom) = F x D(boom)
The boom weighs 6lbs. so that’s the F, but what’s the D?
Remember we’re looking for the line of force which goes through
the center of gravity (CG) of the object. For the load (cylinder) the
CG went through the measured center of the cylinder and it’s the
same for the boom. The CG of the boom is 30″ from the pivot point
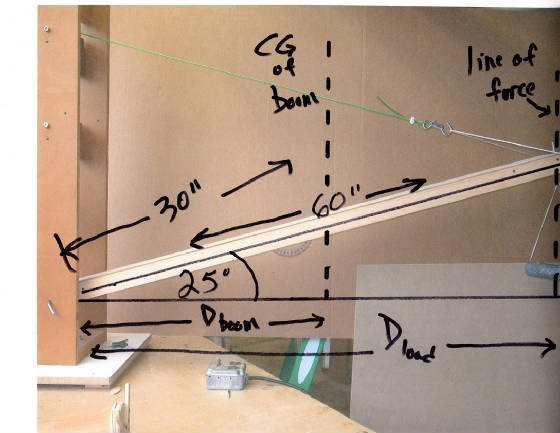
the boom weighs 6lbs. or 96 oz. so that’s the F.
To find the D we use cosine again.
cos 25 = D(boom) /30″ cos 25 = .9063 so
D(boom) = .9063 x 30 = 27.189 inches
M = F x D so
M = 96oz. x 27.189″ = 2610.144 inch ounces
finally
M(load) = 5927.202
M (boom) = 2610.144
TOTAL MOMENT = 8537.346 inch ounces
That’s the total moment trying to pull the boom down .
Now we need an equal moment to KEEP the boom
stationary at 25 deg.
In other words the CW Moment 8537.346 must be equal to
the CCW moment.
Now we work backwards.
8537.346 (CW M) = F x D (CCW M)
We want to find F (the tension in the boom line) but first
we need to compute D, and for that we have to add
more info to our diagram.

If the tower is at a rt. angle to the horizontal, then thecomplementary angle to 25 is 65 deg. Also the cable is55″ long and the distance from the pivot point to wherethe cable attaches to the tower is 40″. The LINE OF FORCE in many of these examples is the
line of force of gravity pulling down on the load, the boom or ?? In this example, the line of force is along the cable. Imagine you’re pulling on the end of the cable to keep the boom fromdropping. Your pulling force is exactly in line with the cable, so the line of force IS THE CABLE, and the Distance is measured at a rt. angle from the line of force to the pivot point.
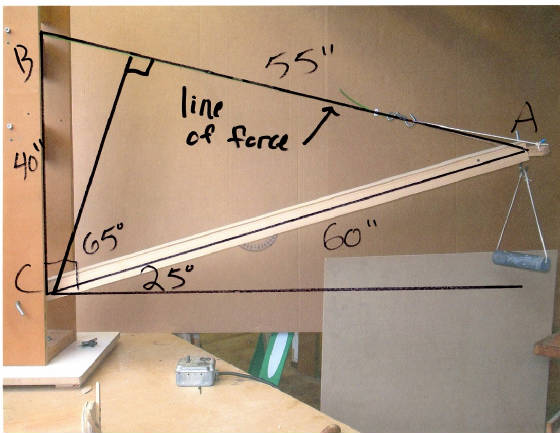
First we have to find the dimensions of triangle ABC
and for that we’ll need the Law of Sines.
a/sina = b/sinb = c/sinc
We already have side a =40″ side c =55″ and
angle c =65 deg. so,
40″/sin a = 55″/ sin 65 and sin 65 = .9063 so
40/sin a = 55/ .9063
sin a = 40 x .9063/55 sin a = .6591 which gives us
angle a = 41.2 deg.
and since there are 180 deg in every triangle, then
angle b = 73.8 deg
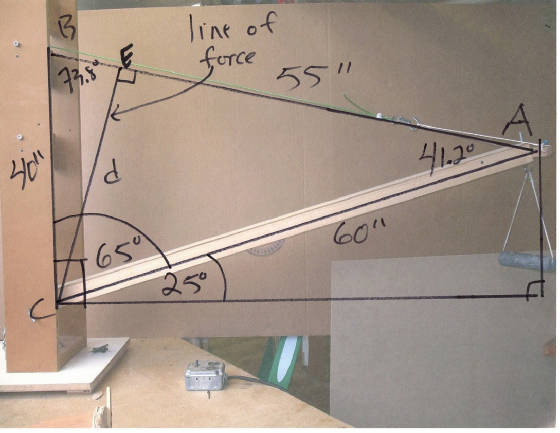
Now all that’s left is to find d or side CE of triangle ACE.
now back to M = F x D
and we already know the value of M 8537.89 inch ounces so
F = 215.897 ounces …convert back to lbs.
sin 41.2 = d/60″ and sin 41.2 = .6591 so
F = 13.493 lbs. or just under 13lbs.8 oz.
8537.89 = F x 39.546 that gives us
We can also use triangle BEC to check our answer.
sin 73.8 = d/40″ you compute the answer.
I got 13.89lbs. or 13lbs. 14 oz.
The load cell reading was …………………13lbs. 12oz.
So we were only off by a few ounces, and considering that
the measurements of the sides of the triangles were not
very exact, and the load cell is also not perfectly
calibrated, a few ounces discrepancy is pretty good.

I made some improvements to the basic crane model

I added a windlass with an automatic brake,and the load cell is connected
to the line going to the windlass.
As the boom is raised the load cell will show the Tension in the line

The load can be placed anywhere along the length of the boom.
