PortlandJib

How do you make sure your crane doesn’t tip over when you lift the load?

What is the line of force and where is the center of gravity?

What formula did Archimedes come up with?

How do we compute TORQUE?

In this first video (15 minutes) I explain how a crane is like a balance beam- you have to know the weights and distances involved in order to safely lift the load.

Now you know the basics. What would happen to the crane if we lowered the angle of the boom from 60 degrees to 45 degrees. You know it will cause the crane to tip over, so we have to run the numbers.

What can we do to prevent a tip over? and what is the safety factor?

Now we can lower the boom to 30 degrees. We’ll need some counter-weight (ct.wt) .

Now that you’re an expert, here’s a situation you might encounter in the field. The load is now 3 bricks, the boom is still at 30 degrees and you have to figure out how much ct.wt. is needed and where to put it.

Now it’s time to use the next crane model. This one has 2 windlasses.

Here’s a crane problem for you. We have to lift a load ( 2 bricks) that are sitting in a box that’s 34″ away from the crane. You have to figure out the boom angle and how much counter-weight (ct.wt.) is needed.

Oh and while you’re at it- I explain what cosine is.

Here’s a series of videos using a different crane model. If you’re learning all about torque, applied trig, overturning moment etc. , these videos will give you another “take” on these topics.

Last year I built my bridge and crane models using 1/4″ plywood that had 3/16″ holes drilled every 1″. I connected members with small plastic angle pieces and 8-32 machine screws.

This model has 2 windlasses- the smaller one raises and lowers the load, while the larger one controls the angle of the boom which is 3 ft long.

I raised the boom to 60 degrees and hung a 4. lb. load (brick) from the hook. The crane immediately tipped over . WHY? We have to run the numbers to find out.
The crane weighs 15 lbs, and the distance from the center of gravity (CG) of the crane to the fulcrum is 9 “. So what. Think of a crane like a see-saw or balance beam.

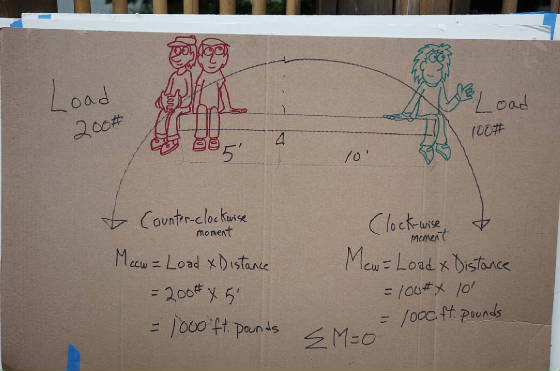
Here’s a see-saw perfectly balanced. But how can 1 guy (100lb) balance 2 guys who weigh 100 lbs. each?

If the green guy sits farther away from the fulcrum than the 2 other guys it will work. If you were ever on a see saw as a kid you’d know this instinctively.

Archimedes came up with a simple formula that can be adapted to show :

WEIGHT X DISTANCE on 1 side must equal weight x distance on the opposite side for everything to balance.

The numbers on both sides are 1000 foot pounds so the see-saw is balanced. Foot pounds…what’s that? The weight ( in pounds) multiplied by the distance (in feet or inches or meters or ???)

200 lbs. times 5 ft = 1000 foot pounds ( or pound feet) of TORQUE When the see saw or the crane moves, it pivots around a fulcrum, so it’s not a straight line movement, but a circular one. If the see saw is not evenly balance and 1 side rotates down ( and the other side rotates up), that movement is circular. Imagine the 2 ends of the see saw trace a circular line. Same with the crane when it tips over. It pivots around the fulcrum- show video.

TORQUE- a force that causes rotation.

The weight of the green guy ( for now assume there’s nothing on the other side of the see saw) makes the see saw rotate around the fulcrum and the further away he is from the fulcrum the more rotational force (torque) he exerts. If this torque is more than the torque of the 2 red guys, then he pivots down and the 2 red guys pivot up.

Now with a crane we definitely want the torque of the crane body to be greater than the torque of the load (and the boom that holds up the load)-otherwise the crane will tip over.

That black triangle denotes the pivot point or fulcrum.

First we need to compute the torque of the crane body ( without the boom and load).

The crane weights 15 lbs. and the distance from the Center of Gravity ( CG) of the crane to the fulcrum is 9″. What’s the CG?

CG= the point where the total weight of the body is concentrated. Imagine the brick that I use as a load. Since all the material in the brick is uniformly distributed we can assume that the CG of the brick is in the center of the brick. An easy way to find the CG is to balance it (the brick or the crane) on a round pipe.

I mark the point on the bric

I did the same thing with the crane and found that the CG was 9″ from the fulcrum.

To find the TORQUE it’s Weight x Distance.

so we multiply 9″ x 15 lbs. to get 135 inch pounds (135″/#)

Next the torque of the load. The brick weighs 4.7 # but what’s the distance? Draw a vertical line through the brick- make sure it goes straight down. That’s the line of force—what force??

GRAVITY . Gravity pulls everything straight down right? To find the distance we measure from this line of force to the fulcrum. But we need it to be the shortest distance and it turns out the shortest distance is a line that’s at a right angle to the line of force.

That line is DL above.

Looks like we’ve got a right triangle- the LINE OF FORCE is the dotted vertical line that goes through the CG of the brick, the hypotenuse is the boom of the crane, and the short line (DL) is the shortest distance from the line of force to the fulcrum. That’s the Distance we need for the formula.

Torque of the load….Weight x distance brick= 4.7# and Dist.= ?

If you’ve watched the previous videos you’ll remember that in a 30-60-90 triangle, the short side (DL) is always half the longest side (hypotenuse). Another way is to use cosine.

Go back and review…cosine =adjacent side/ hypotenuse

the values we have are;

cosine 60 =.5

adjacent side DL (that’s what we want to find)

hyp.=34″ so substituting in we get

.5 = D/34″ and with a little algebra we get Dist. = 17″

Now back to our formula Torque = W x D

Torque = 4.7# x 17″ …. 79.9″/# Let’s call it 80″/# of Torque.

don’t forget the boom. It weighs 2 lbs. and the distance from line of force to the fulcrum is ??? The CG of the boom is halfway along the length of the boom, ( 34″/2= 17 ), so now we have another 30-60-90 triangle but now the hyp. is 17″

Cosine 60 = adj./hyp Cosine 60= .5 adj.= distance we need to find

hyp. is now 17″

So 5= dist/17 and solving we get Dist. =8.5″ and

now back to Torque – W x D we get

Torque = 2# x 8.5″ = 17″/# of torque

which we now add to the torque of the load 80″/# to get

97’/# of torque for the load and the boom. Remember the crane body was

135″/# of torque–much more than the 97″/# for the load , so the crane is safe, it won’t tip over.

But what would happen if we lowered the boom to 30 degrees?

The crane body is still 135″/# and the brick still weighs 4.7# but now it’s farther away from the fulcrum. Again, draw the line of force through the CG of the brick and then another line at right angles that goes to the fulcrum , and do the same thing through the CG of the boom.

Now we have a new right triangle with a base angle of 30 degrees. The boom is still 34″ so that’s the hyp. of the larger triangle, and when computing the torque of the boom, the hyp. of that smaller triangle is 17″.

We’ll still use cosine to find the distance which is the adjacent side of the triangle and cos 30 = .866

cosine = adj./hyp and substituting we get

(cos 60) .866 = dist./34″ dist.= 34 x(.866) = 29.44″ let’s call it 30″

Torque = Wt. x dist so torque = 4.7# x 30″ = 141″/# we’re already over the 135’/# of the crane body.

Now for the boom. it still weighs 2# but the distance has changed. Using the smaller rt. triangle, hyp.= 17″, base angle is 30 degrees and to find the dist. (adj. side) we use cosine again

cos = adj./hyp cos 60 = .866 so

.866 = dist/17″ dist. = 14.72″ now back to torque = w x dist.

torque = 2# x 14.72″………………..= 29.44″/# which we add to the torque of the load (141″/#) to get 170.44″/#, which is way more than the 135 of the crane body.

TIP OVER —what can we do to prevent this? Add counter-weight (ct.wt)

I’ll use another brick (4.7#) but where should we place it? To get the maximum torque, I’ll put it on the far end of the crane body (20″). Remember since torque is W x D, the greater the weight, the greater the torque OR the greater the distance, the greater the torque.

Now to compute the Torque of the ct.wt. the brick weighs —4.7# and the dist is 20″, so 4.7# x 20″ = 94″/# which we add to the 135 “/# of the crane body , and get 229″/#— a lot more than the 170.44″/# of the load and boom.